GEOMETRIA

Índice: Apuntes de geometría.
1.El triángulo 
   2. Lugares geométricos
    3. Movimientos en el plano
    4.Resumen de áreas y volúmenes de figuras conocidas
    5.La esfera y el globo terráqueo
-------------------------------------------------------------------------

1. El triángulo

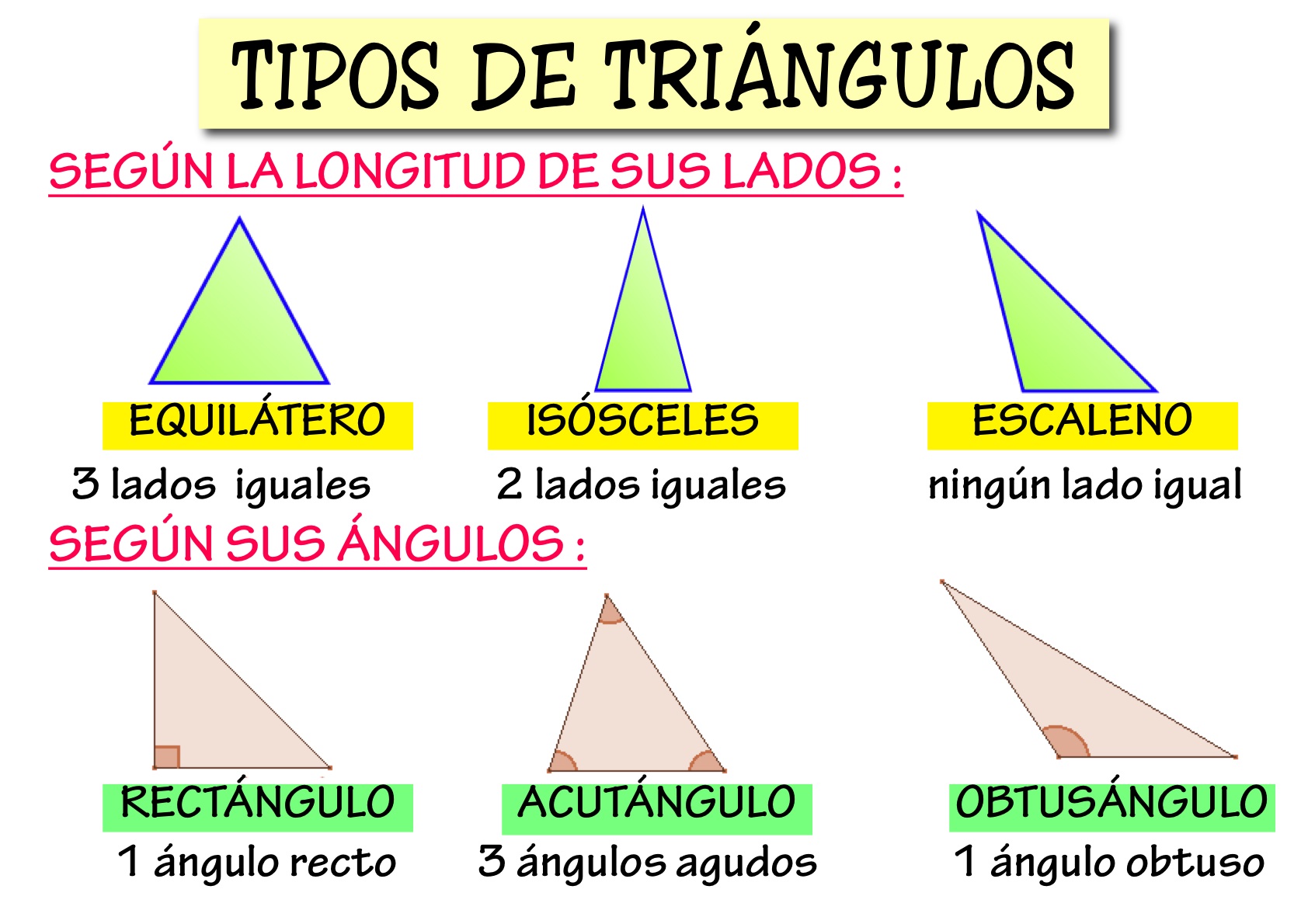
        1.1 Propiedades y tipos de triángulos
                  
   PROPIEDADES DE LOS TRIANGULOS
1 La suma de los ángulos interiores de un triángulo es igual a 180°.
2 Todo triangulo equilátero es equiángulo, es decir las medidas de sus ángulos internos son iguales, en este caso cada ángulo mide 60°
3 Si dos lados de un triangulo tienen igual medida, entonces los ángulos opuestos también son de igual medida
4 En un triángulo a mayor lado se opone mayor ángulo.
5 El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.
6 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su


            

           1.2 Rectas y puntos notables en el triángulo 

El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma.
El baricentro de un triángulo es el punto de intersección de las medianas de dicho triángulo.
El circuncentro de un triángulo es el centro de la circunferencia circunscrita al triángulo, por lo que la distancia a cada uno de sus vértices es la misma.
El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo.

          
           1.3 El teorema de Pitágoras
El teorema de Pitágoras se basa en que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

         1.4 el teorema en 3D
En esta imagen podemos contemplar que el liquido de los cuadrados con aristas que miden como los catetos, corresponde al liquido que cabe en el cuadrado con aristas que miden como la hipotenusa.

El teorema de Tales

  ¿Cómo calcular la altura de un árbol a partir de su sombra?

Sabiendo la altura de un árbol y lo que mide su sombra, podemos calcular la altura de un edificio (si sabemos cuanto mide su sombra) a partir de Tales con una simple "regla de tres".
                                           A'/A = B'/B

2. Lugares Geométricos.
¿Qué es un lugar geométrico?
Un lugar geométrico es un conjunto de puntos que satisfacen determinadas propiedades geométricas.

La bisectriz y la mediatriz :El lugar geométrico de los puntos que equidistan a otros dos puntos fijos es una recta o eje de simetría de dichos dos puntos. Si los dos puntos son los dos extremos de un segmento, dicha recta o lugar geométricos, es llamada mediatriz y es la recta que se interseca perpendicularmente en su punto medio.

La bisectriz es otro un lugar geométrico. Dado un ángulo la bisectriz cumple la propiedad de que todos sus puntos equidistan a los lados de dicho ángulo.

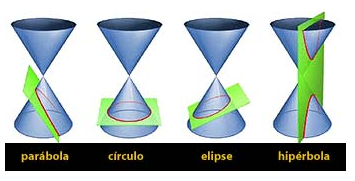
Las cónicas :Son todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

La CIRCUNFERENCIA se obtiene al cortar el cono con un plano de forma paralela a la base.
 LA ELIPSE
La elipse se obtiene al cortar el cono de forma secante a los lados del cono, tal y como se ve en la imagen.

Para dibujar una elipse con el metodo del jardinero:

Primero debemos dibujar perpendicularmente los dos ejes de coordenadas en el suelo.
Luego debemos de señalar los dos focos.
Despues, con una cuerda que tenga de longitud l = 2a y colocando los extremos en los focos señalados, dibujamos la elipse.

En una mesa de billar eliptica, si colocas una bola en un foco y otro en el otro foco, siempre golpearas la bola. 

LA HIPÉRBOLA

La hipérbole se obtine al cortar de forma perpendicular a la base los dos conos.
La luz que emite una lampara, produce como dos conos, que al cortarse con la pared, forma una hipérbola. (Lo podemos observar en estas imágenes).
LA PARÁBOLA
La parábola se obtine al cortar de forma paralela al lado del cono y que pase por su base.

LA ANTENA PARABOLICA

En las antenas parabólicas, la así llamada parábola refleja las ondas electromagnéticas generadas por un dispositivo radiante que se encuentra ubicado en el foco del paraboloide. Los frentes de onda inicialmente esféricos que emite ese dispositivo se convierten en frentes de onda planos al reflejarse en la parábola, producen ondas más coherentes que otro tipo de antenas.

Un horno solar es una estructura que usa energía solar concentrada para producir altas temperaturas, usualmente para usos industriales. Hay varios tipos, uno de ellos son los reflectores parabólicos o helióstatos. Estos concentran la luz sobre un punto focal para calentar la comidaualmente para usos industriales.Un espejo parabólico tiene la particularidad de que todos los rayos que llegan paralelos al eje óptico se reflejan pasando por el foco. Esta característica se aprovecha por ejemplo en la construcción de antenas parabólicas, hornos solares, etc. 

De la misma manera todos los rayos que pasen por el foco se reflejan en el espejo saliendo paralelos al eje. Podemos observar esta propiedad al observar los faros de un coche, en ellos la lámpara se coloca en el foco de manera que al salir los rayos de luz paralelos al eje la luz se concentra en la dirección de la carretera.

Este comportamiento lo presentan sólo los espejos parabólicos, aunque también puede considerarse que se comportan así los espejos esféricos cuando corresponden a una pequeña sección de esfera. De hecho, a lo largo de la historia la gran mayoría de los espejos construídos han sido esféricos, porque resultan mucho más fáciles de construir.

3. Movimientos en el plano
 
 En geometría, una TRASLACIÓN es el movimiento de cada punto a una distancia constante en una dirección dada.En matemáticas, se define un VECTOR como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo.
4. Resumen áreas y volúmenes:

5.La esfera y el globo terráqueo

5.1 Elementos principales de la esfera

• Centro: Punto interior que equidista de cualquier punto de la esfera.
• Radio: Distancia del centro a un punto de la esfera.
• Cuerda: Segmento que une dos puntos de la superficie.
• Diámetro: Cuerda que pasa por el centro.
• Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica. 

         5.2Elementos de laesfera terrestre.

 

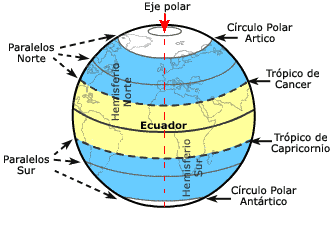
• Meridiano de Greenwich: También conocido como meridiano cero, meridiano base o primer meridiano, es el meridiano a partir del cual se miden las longitudes. Se corresponde con la circunferencia imaginaria que une los polos y recibe su nombre por pasa por la localidad inglesa de Greenwich, en concreto por su antiguo observatorio astronómico.

• Ecuador: Es el plano perpendicular al eje de rotación de un planeta y que pasa por su centro. Divide la superficie del planeta en dos partes: el hemisferio norte y el hemisferio sur. Por definición, la latitud del ecuador es 0°

TRABAJO DE FUNCIONES (fisgoo)

Hoy vamos a realizar un trabajo subido a la pagina web fisgoo:

1ª PARTE: Conceptos básicos  

1- . ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo? 
  -Mediante un eje de coordenadas 

 2- ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc. En las figuras siguientes tienes 3 ejemplos:

 -En análisis matemático, el concepto general de función, aplicación o mapeo se refiere a una    regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo    conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único    cuadrado, que resulta ser un número natural (incluyendo el cero) se pueden expresar      mediante tablas, gráfica, ecuaciones o formulas ejemplos:

3- ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder.
-Es el incremento de una función, que mide lo que cambia al pasar de un punto a otro. En las crecientes, toma un valor superior a 0 (positivo), y, en las decrecientes, toma un valor menor a 0 (negativo).

4- Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos.
El Mínimo Relativo en Una función f es el punto Donde la variable de evalúa Que Toma El valor Más Bajo en un Intervalo Determinado, MIENTRAS Que El Mínimo absoluto es el punto Donde la variable de Toma que evalúa El valor Más Bajo INDEPENDIENTEMENTE del Intervalo.

5-Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría. 

Se dice que una función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la función es impar.


6- Representa gráficamente una función periódica indicando por qué se denomina de esa forma. 





Las funciones periódicas son aquellas en las que tienen ondas que muestran periodicidad respecto al tiempo, es decir, describen ciclos repetitivos.



 

7-Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas?

Función discontinua: Una función es discontinua cuando su función f es definida en un intervalo abierto y es interrumpida.

Función continua: Una función es continua cuando su gráfica es una linea seguida, no interrumpida


8-Investiga: ¿Cuál es el origen del término función?

No apareció hasta los inicios del cálculo en el siglo XVII. René Descartes, Isaac Newton y Gottfried Leibniz establecieron la idea de función como dependencia entre dos cantidades variables. Leibniz en particular acuñó los términos «función», «variable», «constante» y «parámetro». La notación f(x) fue utilizada por primera vez por A.C. Clairaut, y por Leonhard Euler en su obra Commentarii de San petersburgo en 1736.

 2ª PARTE: Estudio y representación de funciones

9. Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora un tabla resumen con todas las gráficas obtenidas.

a) Función lineal creciente:

b) Función lineal constante:

c) Función lineal decreciente:














d) Rectas paralelas:

e) Función cuadrática cóncava:

f) Función cuadrática convexa:

10. Investiga sobre la representación de funciones en coordenadas polares

Las coordenadas polares o sistemas polares son un sistema de coordenadas bidimensionalen el que cada punto del plano se determina por una distancia y un ángulo. Este sistema es ampliamente utilizado en física y trigometría.


12. Utiliza el programa que has elegido para resolver gráficamente el sistema de dos ecuaciones lineales con dos incógnitas siguiente: 
3x -2y = 4
2x +3y = 33                            resultado {  y = 7 ; x = 6  }